AI（人工知能、artificial intelligence）ということばは、ここ数年で本当に身近になった。ちょっとしたソフトやアプリであれば、AIということばが入っている。一日に何度も目にする。AIはあと数十年で、いわゆるシンギュラリティ（技術的特異点）を越え、人間の知能を身につけるともうわさされている。

 

ところが、実はAIとは何のことだか誰もわからない。「ちょっと賢い人間みたいなコンピューター」というのが多くの人の定義だろう。一般向けの解説本で何度か、この定義を目にしたことがある。しかし、これでは具体的な説明になっていない。

 

もちろん専門家ならAIとは何かがわかっている。しかし、ここには大きな問題がある。実は専門家でもAIが何かは、わかりやすく説明できないのである。

 

ちょっと古いが下の記事が昨年話題になった。ディープラーニングというAIの技術についての説明に関する記事である。

 

＜引用開始＞

「ディープラーニングは、原理的には単純な最小二乗法にすぎない」――2月18日付けで日本経済新聞電子版が公開した記事について、Twitterでは「ディープラーニング＝最小二乗法」という解釈は異なるのではという指摘が相次いだ。19日には「ディープラーニング」「最小二乗法」といったワードがTwitterでトレンド入りし、波紋が広がっていた。

 

日経の記事では、慶應義塾大学経済学部の小林慶一郎教授がAI技術について解説。「近年、驚異的な発展を見せているAIのディープラーニング（深層学習）は、原理的には単純な最小二乗法（誤差を最小にする近似計算の一手法）にすぎない」と言及し、「ディープラーニングは『最小二乗法』」と題する図版が掲載された。

 

最小二乗法は、測定で得られたデータの組を、1次関数など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、モデル関数の値と測定値の差の2乗和を最小とするような係数を決定する方法。ディープラーニングに詳しい東京大学の松尾豊特任准教授は、2018年8月に登壇したイベントで、「ディープラーニングは最小二乗法のお化けのようなもの」「従来のマシンラーニングは（階層的に）『浅い』関数を使っていたが、ディープラーニングは『深い』関数を使っている」と説明していた。

 

松尾氏は2月20日、Twitterの公式アカウントで「小林慶一郎先生はよく議論させていただくので、少し責任を感じています」とツイート。ディープラーニングを簡潔に解説するため「深い関数を使った最小二乗法」という言葉を使ってきたが、「深い関数を使った」という説明がいつも抜け落ちてしまうと嘆く。

 

続けて、「深い関数により表現力が革命的に上がり、アルゴリズム的な挙動も含め表現できるのは驚くべきこと」「『最小二乗法』は、損失関数を最小化することで、モデルのパラメータをデータから推定すること（略）深いことに比べるとそれほど重要ではありません」と投稿。経営者や政治家など、AIに詳しくない非エンジニアに正しく理解してもらうための解説は「大変難しい」と痛感しているようだ。Twitterでも同様に、AI技術について上司や同僚にどう解説すればいいかを嘆くエンジニアの声も見られた。

ITmedia NEWS

「ディープラーニングは最小二乗法」で物議　東大・松尾豊氏「深い関数の方が重要」より引用

＜引用終了＞

 

ここで、書いておくとこの小林教授の「ディープラーニングは最小二乗法」という発言は正しい。それに対して、松尾豊氏の「深い関数」という発言はよくわからない。

 

理科系の人間はこんな感じだ。「おまえがわからなくても、それはお前がわるいんだから、俺は知らないよ」みたいな感じで突き放して書く。上の記事は典型的なその例のひとつだ。

 

実は松尾豊氏のいう「深い関数」は誤訳である。本当は「×深い関数」ではなくて「〇厚い、多層の関数」というのが正しい。ｙ＝ｆ（ｇ（ｈ（ｘ）））みたいな関数だ（これだと３層）。実際、Deep learning ということばがあるが、これを「×深い学習」とはあえて訳さず、「〇深層学習」と訳してある。

 

さて、こんな感じで専門家でもAIが何かは（この場合はディープラーニング）、わかりやすく説明できない。いろいろな本や記事を読んだが、未だにAIとは何かをきちんとわかりやすく説明した文章はない。あるAIの専門家が「AIを学ぼうと思ったら5日かかりますから、きちんと全部勉強してください」みたいな高飛車なことを、大企業のお偉方に述べた記事を見たこともある。

 

そこで、AIとは何かを私が昔に書いた本の記事をもとに詳細にわかりやすく説明する。そして、いまはやりのAIのアプリケーションソフトであるｃｈａｔＧＰＴを有名なmathematica（マセマティカ）というソフトを開発したスティーブン・ウルフラムの解説文を参考に説明する。

 

しつこいようだが、AIとは何かをだれもわかっていない、専門家は説明できない。だから、もしこれを読んでいる方が、「なるほど、AIとは、こういうものなのか」と理解できれば、それは、その人の人生にとってものすごくためになる。

 

もし理解できれば（文系の人は特に）、今後、AIの話題が出てきたときに、「あーそうか、そうやって、応用することができるんだ」と仕組みまで納得することができます。本当です。

 

 

さて、AIを説明する前にAIを定義しておこう。キチンとことばの定義づけすることで、理解がすすむ。実は、AIとは、

『人間の経験を数値化するための数学的技法』

のことである。

 

数学的技法にいろいろある。高校で習う微分、積分、大学の時に習うベクトル解析もみんな数学的技法のひとつである。AIもそのうちのひとつである。だから賢いコンピューターとかそういうことではない。そして、そのやり方（アルゴリズム）が極めて、「最小二乗法」に似ているということに他ならない。

 

もし、この文章を最後まで読んで、「AIとは、実は、『人間の経験を数値化するための数学的技法』のことである。」ということばを、「あーなるほどなー、確かにそうだ」と素直に納得できたなら、あなたはAIを完璧に理解できたと考えることができます。

 

長くなるので、次回に続きます。

下條竜夫拝

さて、ここでは私が昔書いた本、『物理学者が解き明かす思考の整理法』で記述した将棋のAI導入の方法を詳細に説明する。それによってAIとは何かが理解できる。

なぜ、将棋を扱うかというと、将棋のAIだけが、どのような数学的な技法をつかっているかが、よく理解できるからである。その他のAI、例えば画像解析もchatGPTもディープラーニングという方法を使っている。そのため、そのパラメーターが何をあらわしているのかが専門家でもわからない。もっと言えば、なぜよく解析できるかもわかっていない。したがって、その仕組みの説明を聞いても、しろうとには、さっぱりわからない。

そこで将棋である。

将棋はおよそ10の220乗の変化があるから、数十手すすむと、もう今までに指したことない未知の手が当然でてくる。ということは通常のデーターベースによるコンピュータープログラムでは、新しい局面がでてきて対処できない。

そこでゲームとして将棋をプログラミングする場合、次のようにプログラミングする。

①ある局面とその数手後までを数値化する。

②ある系統の中で最低値が最大になる系統をえらび次の手を選択する。

これを、ミニマックス探索、そして、ある系統の中で最低値を「ミニマックス探索値」とよぶ。つまり、相手がベストの手を指すと予測して、その中で一番いい手を選ぶようになっている。

だから将棋ソフトをつかっていると点数や勝利の確率が表示されるが、あれは、その時次にベストの手を指すと仮定した値が必ず表示されている。だから、いい手を指したとしても数値はよくならないし、悪手を指したときだけ相手の評価があがる。そういう仕組みになっている。

さて、上記の「①ある局面とその数手後までを数値化する」というのをもっと詳しく見てみよう。

この数値化の方法にはいろいろある。いちばん簡単な方法は、持ち駒の種類と数とか、自分の２つの駒の配置とかである。これを数値化してすべて足す。相手より点が多ければ、その差の点数だけ有利ということになる。

この数値化したものを「局面評価関数」という。これはどのゲームでも同じで、例えば、オセロという表裏が白黒の駒をひっくり返して、コマ数を争うゲームがある。このオセロでは、主に、同じ色の直線ができると高い局面評価関数が得られるようになっている。

将棋では、上に書いたように駒の配置と持ち駒が局面評価関数の指標となる。

この指標こそがAIで「特徴表現」と呼ばれるものである。

つまり、表現（representative　＝　代表）とは、ゲーム中の優勢劣勢を決めるために、数値化して代表した様々のパラメーターに他ならない。この指標の呼び方は、特徴表現だけでなく、評価パラメーター、特徴ベクトル、特徴量などいろいろある。ベクトルはその指標の数を次元として表せる。だから、十個の指標があれば「十次元のベクトル」として数学的にあらわされるのでベクトルと呼んでいるようだ。

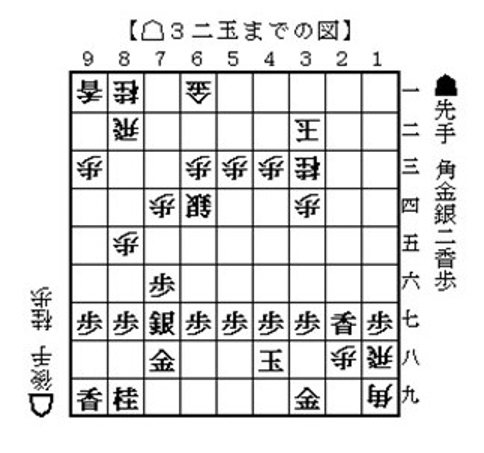
この「特徴表現」は、持ち駒の種類とか、持っている２つの駒の配置とか、飛車や香車がどれほど動けるかなどの状況を得点としたものである。わかりやすく、例をあげておく。次図に示したのは、玉と金との関係で、王が８八（上）と９九（下）にある時の金の位置に対する得点つまり特徴表現である。見てわかるとおり、王に近いところに金がある、つまり守りが固いほど得点が高いということがわかる。

将棋が得意な人にはよくわかる図である。

さて、具体的に見てみる。今、図で王が８八にあるときに、金が６八から７八に移動したとする。すると、特徴表現のパラメーター値（特徴表現の数値）は－１６から３０に変化する。当然、他の特徴表現（金と銀の関係など）のパラメーター値も変化するから、それも合算する。つまり、このような特徴表現のパラメーター値がたくさんあり、指手により変化したすべての特徴表現のパラメーター値を合計して、局面評価関数とする。他には次のようなものが特徴表現となっている。

「王，他の駒２つの位置」、「王，隣接した味方の駒、他の味方の駒３つの位置」、「隣接しあった駒２つの位置関係」、「竜馬飛角桂香の利き上にいる駒の種類」、「竜馬飛角香が動ける枡の数」、「ピンされている駒の種類，方向，王との距離」、「角と同じ色の枡にいる味方の歩の数」、「歩桂銀が前進できるか」、「竜飛香の前・後の歩」、「王の周囲25枡の利きの配置」となっている。

これをすべて数値化して単純に足して局面評価関数とする。相手も同様に足して多い方が点が高く有利であることをあらわす。

実は、ここまではAIとはまったく関係がない。ここからがAIの出番である。

つまり、ここで問題がひとつでてくる。先ほどの図のパラメーター値（特徴表現の値）をどうやって決めたらいいのだろうかという問題だ。適当に決めてもいいが、それでは将棋の強いソフトとはならない。

保木邦仁氏という人は、「機械学習」という方法を用いて、これらの得点を決めた。具体的には、プロ棋士の対局データ六万局をもとにこの得点を決定した。つまり、「六万局の棋譜の指手を参考にして、プロ棋士が選択した指手が最良となるように特徴表現のパラメーター値（先ほどの図（王と金の関係）の得点）を決めたのである。」

このように過去のデータを自動的に処理させ、プログラムの機能を向上させる方法を「機械学習」という。これが２つめのキータームの「機械学習」である。

さて、さらに実際の特徴表現の得点の決め方を見ていこう。

６万局のプロ棋士の将棋対局、一局百手として約６００万の指手がある。これについて先ほどの特徴表現を最適化してみよう。

下の将棋のある場面を見てほしい。

この局面でプロの指手が一手、　この局面でプロが指さなかった指手＝数十手があるとしよう。そして、この局面でプロの指手よりも大きな局面評価関数（＝ミニマックス探索値）を示した手の数を「目的関数」とする。つまりプロが指した手よりいい評価を示す指し手の数が評価関数である。通常プロがいちばんいい手を指すとすれば、０かあるいは１とか小さい値だろう。

これは上の局面だけであるが、同様に６００万手についてすべて同じことを行い、６００万手についてこれらをすべて足し合わせる。そしてそれを誤差関数とする。

今やりたいことは、プロ棋士が選択した指手が、他のどの指手よりも評価関数の値（ミニマックス探索値）が高くなるようにすることだ。これは、この誤差関数ができるだけ小さければいい。つまり、すべての特徴表現のパラメーター値をいじって変化させ、できるだけこの誤差関数を最低になるようにすればいい。

つまり、先ほどのすべての特徴表現のパラメーター値を少しずつ変化させ、この６００万の指手について足し合わせた誤差関数が最小になるように特徴表現のパラメーター値を決定するわけだ。これは最小勾配（こうばい）法と呼ばれている。

すると、「プロ棋士が選択した指手が最良となる」ということは、「６００万手について合計した誤差関数が最低値（停留値）をとるように特徴表現の得点を決定する」という数学命題に変わる。これなら、コンピューター計算でできる。

そして、一度、この特徴表現のパラメーター値が全部決定して完成してしまえば、それをつかって、まったく新しい将棋の局面でも、合計した値である局面評価関数値をミニマックス探索して、指手が決定できる。

現在ではプログラムの動作を決定づける１千万以上の特徴表現パラメーター値の最適化を行っていると書いてあるのを雑誌の記事で見たことがある。

まだ続きます。

下條竜夫拝

さて、副島先生が重要な投稿を次々としているので、つい邪魔をしてはいけないと思って期間があいてしまった。すみません。

前回の将棋ソフトをプロ並みにする「機械学習」という仕組みが理解できれば、ＡＩという技術そのものがわかったことになる。もし忘れていたら、もう一回読んでほしい。

つまり、将棋のプログラムの中で使われた「機械学習」による「特徴表現のパラメーター値の決定」がＡＩの本質である。将棋をやったことがある人ならだれでもAIの仕組みが理解できるだろう。そこが重要だ。

 

もう一度確認しておこう。

まず、膨大な数の「特徴表現」を設定する。将棋なら「持ち駒」とか「王と金の位置関係」などが対応する。その特徴表現のパラメーター値を、「教師」（将棋で言えばプロ棋士の対局）を参考として、「機械学習」によって膨大なデータから決定する。その場合、評価関数とそれを合計した誤差関数というものを定め、それが最低になるように少しずつパラメーターの値を動かし最適化する。

この数学的技法のことを「AI」を読んでいるわけだ。一回パラメータがすべて決まれば、どんな新しい局面にも対応できる。

 

さて、今まで述べてきた将棋では、どの特徴表現（特徴ベクトル）を利用するかは、人間が決めている。しかし、最先端のAIでは、機械自らがこの特徴表現（特徴ベクトル）を探し当て決定していく。

そして、それを可能にしたのが、深層学習（ディープラーニング）という方法である。「多段階のニューラルネットワーク」とも呼ばれる。

今１，２，・・・・９までの画像上の数字を、どの数字か認識させる場合を例に考えてみよう。例えば、手書きの３という数字を考えてみる。汚い字は、この３が極端に歪んでいる。このままでは機械で認識できない。そこで、画像素子上でその汚い３を読み取った後、素子に重みをかけ、まわりの素子と足しあわせて変形していく。そして、そうした演算を何段階も行い、最後に３と認識する。

つまり、タテ３２×ヨコ３２（合計１０２４個）の画像素子があるとすれば、これを「入力」、最後１から９までの９個を「出力」として設定する。出力が一番大きな数字をその数字の画像と判断するわけだ。

機械学習としては、すでにある１００枚とか１０００枚の画像をつかう。これがすべて正解になるように上の「重み」と「足し合わせ」をパラメーターの値として変形していく。実際の画像と結果の違いを「誤差関数」として将棋の時と同様に、誤差関数が最小になるようにパラメーターの値を調整すればいい。

ただし重要なのは将棋と違い、深層学習（ディープラーニング）では、この特徴量つまりパラメーターが何を意味するかさっぱりわからない点である。つまり、他の人にどのような過程をへて計算しているか、まったく説明できない。だからAIとは何をしているのかが、ほかの人に説明できない。

 

さて、生成AIについても簡単に説明しておこう。

生成AI（Generative Artificial Intelligence）とは、学習したデータをもとに、文章などの新たなデータを生成する人工知能（AI）である。代表的なのが chatGPTというソフトである。

「生成AI＝chatGPT」というのはあたかも人間の思考のように新たな文や文章をうみだしているように見える。しかし実際にやっていることは、将棋のAIソフトと同じである。これを大規模にやっているだけにすぎない。将棋のパラメータ数が数千万、chatGPTでは数億から数百億である。

以下、スティーヴン・ウルフラムという有名な数学ソフト（Mathematica）の開発者が書いた本『ChatGPTの頭の中』という本から抜き出してその原理を説明してみよう。

＜引用開始＞

何よりもまず押さえておきたい点がある。ChatGPTは基本的に、そこまで出力された内容の「順当な続き」を出力しようと試みるということだ。「順当」とは「億単位のウエブページなどに書かれている内容を見たうえで人間が書きそうだと予測されるという意味である。

＜中略＞

ChatGPTで驚異的なのは、たとえば小論文を書くときなどでも、基本的には「ここまでの文を受けて、次に続く単語は何か？」という質問を繰り返し、そのたびに１つずつ単語を追加しているにすぎないということだ。

＜引用終了＞

つまり、ChatGPTは次々に単語を足していって文章をつくっていることになる。

これは、極論すれば、将棋と同じことをしていることを意味する。将棋では場面場面で、何百手あるうちのある一手を選択する。ChatGPTは、数万あるうちからひとつの単語を選んで、単語の列につなげていく。つまり次に続くいちばんふさわしい単語と判断して、それを選択してつなげる。生成AI＝chatGPTは文章をつくっているように思えるが、実際は単語をつなげているだけなのである。

ただし、将棋との違いは、単語そのものがベクトルと呼ばれる値そのものをもっているところにある。これにより単語の意味がちかいなどの判断ができる。

＜引用開始＞

極論すれば、単語の特徴を数百から千単位、万単位の数値のリストによって表現している。これを埋め込みベクトルというが、元の形のままではあまり情報として利用できない。しかし、このようなベクトル間の距離を測るなどの処理を経ると単語どうしが「近いかどうか」などを確かめることができる。

＜引用終了＞

 

以上、三回にわたってAIについて説明してきました。皆さんの生活、仕事に役立てていただければ幸いです。

下條竜夫拝

』