②『生命は器械ではない』「最後の講義 完全版 どうして生命にそんなに価値があるのか 福岡伸一」

「

第２章

１年前の自分は別人である

 

食べ物は体で何になる？

シェーンハイマーは、この実験をもっと別の角度からも行いました。

絶え間のない合成と分解によって、食べ物の原子や分子と自分の体の中は交換されています。爪や髪の毛、皮膚が交換されていることは実感しやすいでしょうけれど、体のあらゆる部分は例外なく入れ替わっています。そして、交換は部位によって早い遅いがあるのです。皆さんは、自分の体の仲で最も速い速度で入れ替わっているところはどこだと思いますか？シェーンハイマーはいろいろな部位を実験し、どこがどれくらいの速度で入れ替わっているかを調べました。いちばん早く入れ替わっているのは、消化管の細胞でした。胃や小腸や大腸です。表面の細胞はだいたい２日か３日で分解され、捨てられていたのです。同時に、食べ物から食べた原子や分子によって合成された新しい細胞が配備され、消化管の細胞を作っていきます。ですから、体内から排出されるうんちの主成分は食べ物のかすではなく、分解され、捨てられた細胞のかすなのです。

消化管は２、３日で入れ替わっています。他の臓器も早いお阻医歯あれ入れ替わっていて、筋肉だと２週間ぐらい、血液の細胞だと数か月で入れ替わります。骨や歯のように固まっているように見える部位でも中身は入れ替わっています。脳細胞も細胞と細胞の配置は変わりませんが、細胞の中身は入れ替わっています。

したがって、「昨日の私」と「今日の私」は少しだけ入れ替わっているといえるのです。数週間も前の私とでかなりの部分が入れ替わっています。数か月もたつと相当な部分が入れ替わり、１年前の私と今日の私ではほぼ別人になっています。物質レベルではほとんどが入れ替わっているといっても過言ではないほど替わってしまっているのです。だから、１年前の私が言ったことは別人が言ったことですから。

そんな冗談が言えるぐらい私たちの体は流転しているというか、動いているのです。その様子を、シェーンハイマーはアイソトープを使って可視化したわけですが、可視化するまでもありませんでした。環境中のものが自分の体の中に流れ込んできて、一瞬、体内でよどみ、流れ去っていくその様子はまさに、『方丈記』の冒頭にある、「ゆく川の流れは絶えずして、しかも、もとの水にあらず。よどみに浮かぶ泡末は、かつ消え、かつ結びて、久しくとどまりたるためしな」という描写が示していたのです。まったく同じことが、生命の真っただ中で行われていたのです。

 

方丈記

歌人・鴨長明によって鎌倉時代に書かれた随筆。晩年、京都郊外の庵に暮らしながら、世の中を観察して書き記した。『徒然草』『枕草子』と並ぶ古典の「三大随筆」に数えられる。

 

動的平衡とは？

皆さんは、自分の体は固体だと思っているでしょう。でも、少し長い時間軸で見てみると、絶え間なく流れている流体だということがわかります。流れ去るとともに、作り替えている。シェーンハイマーはアメリカに渡った研究者なので、これを英語で「ダイナミックステイトに私たちの体はある。動的な状態にある」と論文に書いています。このコンセプトこそが、ミクロなプラモデルみないな部品で私たちができているという機会論的な生命観ではなく、私たちの体はもっと流動的に、絶えず動いているという生命観を教えてくれたのです。

それに気づいた私は、シェーンハイマーのコンセプトを日本語では「動的平衡」と呼べばいいのではないかと考え、提唱することにしました。

「動的」とは、常に動いているということです。「平衡」はバランスを意味し、絶え間ない流れの中で、常に合成と分解がバランスをとっていることが私たちの体のいちばん大事な特性で、「動的平衡があるから、生命たらしめられている」ということができるのです。

動的平衡の特徴は、作ることよりも壊すことを一生懸命にやっているということ。２０世紀の生物学の研究者は、細胞がいろいろなものを作るメカニズムを研究してきましたが、２１世紀になると、実は細胞は作ることよりも壊すことを一生懸命やっていることが次々とわかってきたのです。

２０１６年に大隅良典先生がノーベル生理学・医学賞を受賞されました。大隅先生の研究テーマは「オートファジー」です。細胞の中でいかにタンパク質が分解されるかという仕組みを明らかにされましたが、その仕事は、作ることよりも壊すことが大切だということを見事に言い当てておられました。そこには「動的平衡の生命観」が流れています。

絶え間のない流れの中で合成と分解を繰り返しているさまは、「変わらないために変わり続けている」と言い表すこともできます。矛盾したように聞こえますが、大きく変わってしまわないために、常に小さく変わり続けているのが私たちの体なのです。常に合成と分解による動的な平衡が成り立っているから、私たちの体の中は何かがなくても他のものがピンチヒッターとしてやってきて、平衡状態を作り直すことができるのです。それくらい、生物というものは柔軟にできているのです。環境が変わればそれに適応して体を変えることができます。病気や事故があっても回復することができるし、傷があれば修復もできるという、生命の持っている可塑的な特性は動的平衡が成り立っているからこそ発揮されるものなのです。

では、どうして私たちの体は絶え間のない動的平衡の中にあり、去年の私と今年の私は物質レベルではすべて入れ替わっているにもかかわらず、「私は私である」という自己同一性が保てているのでしょうか。何十年も前の記憶が保存されているのも不思議です。物質が入れ替わったら、記憶が失われてもおかしくないはずです。でも、そうはなりません。生命は動的平衡のバランスによって自分自身がそう簡単に変わらない仕組みを持っているからです。その仕組みは「相補性」です。私たちの体は互いに他を補い合い、支え合いながら律しているのです。

ジグソーパズルを思い起こしてください。私たちの体の中の細胞や、細胞の中のタンパク質も、ジグソーパズルのピースのように前後左右上下の関係性の中で成り立っているのです。私たちの体は非常に大きなジグソーパズルのようなものとも考えられます。

今、ジグソーパズルの真ん中のピースが１つ分解され、捨てられてしまったとしましょう。でも、そのまわりの８つのピースが残っていると、捨てられたピースのかたちはそこだけ切り抜かれたように保存されます。すると、そのかたちに合わせて新しいピースができ、そのピースがどこにはまればいいかが自動的に決まってきます。これが相補的な関係です。私たちの体を構成する「ジグソーパズル」のすべてのピースについて相補性が成り立ち、体のあちこちで同時多発的にピースの交換が行われているのです。

食べ物の元気や分子と私たちの原子や分子も、パズルのピースのように交換されています。細胞も交換されていますが、相補性が成り立っている限り、私たちの体は大きく変わることはありません。ミクロなパーツのレベルではどんどん入れ替わっていますが、パズル全体の図柄は相補性によって支えられているので大きくは変わりません。ただ、大けがをしたときのようにごっそりとピースがなくなってしまうと相補性が失われ、元どおりにならないこともあります。それでも、基本的には私たちの体は相補性によって支えられていますから、自己同一性が保てる理兪も説明できるのです。

 

オートファジー

自食作用のこと。ミトコンドリアや輸送小胞など細胞内にある構造体を特殊な膜によって取り囲んで隔離し、酵素を送り込んで分解してしまう。分解された産物はリサイクルされたり、排泄されたりする。つまり、エントロピーが捨てられる。大隅チームは、酵母という微生物をモデルに使い、オートファジーのメカニズムを明らかにした。

 

動的平衡では、まわりの８つのピースが、欠けた１つのピースの役割を埋めるという「相補性」が発揮される。

 

自らを壊す生命

もうひとつ、なぜ私たちの体が、絶え間なく自分自身を壊しながら作り替えなければならないのかというと、それは、「エントロピー増大の法則」と戦わなければいけないからです。エントロピー増大の法則は少し難しく聞こえる言葉ですが、宇宙のシンプルな大原則で、秩序のあるものは秩序がない方向にしか動かないという法則です。エントロピーは「乱雑さ」と訳しますが、例えば、きれいに整理整頓した机の上も２、３週間もすればだんだん紙が積み重なってきたり、本が崩れてきたり、コーヒーの染みがついたりして、乱雑になってきます。これを、「エントロピーが増大した」といいます。宇宙の大原則ですから、それは仕方がないことです。

建てた当時はみんなが仰ぎ見るような壮麗で石造りの建物も、数百年、数千年の時の流れの中でエントロピーが増大すると、砂粒の風化した建物に変わってしまいます。いれたてのコーヒーは熱々で薫り高いものですが、１０分もたてばぬるくなります。熱烈な恋愛もコーヒーのように冷めてしまうのはエントロピーが増大するからです。

生物は常にエントロピー増大の法則に脅かされているのです、細胞はいつも酸化して壊れそうになったり、老廃物がどんどんたまったり、タンパク質も変性したり、切断してしまいそうになっています。つまり、秩序があるものは秩序がない方向にしか動かないという宇宙の大原則に対して、生命は常に必死に抵抗しているのです。実はそれが、生命が存続している理由であり、方法でもあるのです。

普通、物を長持ちさせようと思えば頑丈に作ります。家やビルも基本的には頑丈に、風雪に耐えるように建てます。ただ、都心に建っている高層ビルやタワーマンションも、竣工した当時はピカピカに見えますが、３０年もたつとどこかが傷んできますし、３００年たつともう住めなくなり、３０００年たつと跡形もなくなっているに違いありません。けれども、生命は３８億年もの長い間、なくなることなく連綿と続いています。

なぜ、生命だけがエントロピー増大の法則に逆らって生きながらえているかというと、最初から頑丈に作ることを諦めて、自分自身うぃゆるゆるやわやわに作っておき、それを常に分解して、捨てて、作り替えるという戦略をとったからです。エントロピー増大の法則が襲ってくるよりも先回りして、自分自身を積極的に壊し、作り替えるという動的平衡を繰り返すことによって、秩序を作り直し続けているから生命は存続できているのです。生命を動的平衡として見ることで、なぜ生命が長い間、存在し続けているかも説明できるのです。

それを、１００年以上も前のフランスの哲学者、アンリ・ベルクソンは著書『創造的進化』の中で、こんな言い方で解説しています。「生命には物質の下る坂を上ろうとする努力がある」と。もう少しわかりやすく言い換えると、「下り坂を上り返そうと頑張っているのが生命だ」といえますが、動的平衡の考えにしたがって、この言葉をより解像度の高い言葉で言い直すことができると思い、私は今、理論的な研究を行っています。それが、ここで紹介する動的平衡の数理モデルです。

万有引力の法則によって、高いところかにある物は放っておくと坂を下って低いところに落ちていきます。もちろんそれは、エントロピー増大の法則とは単位系が異なるので物理的には直接重なり合うことはありません。便宜的に、高い位置エネルギーにある物質が低い位置エネルギーにある物質へ落ちていく万有引力の法則と、秩序の高い状態が徐々に崩壊して秩序の低い状態に陥るエントロピー増大の法則を同じものと見なして考えてみます。

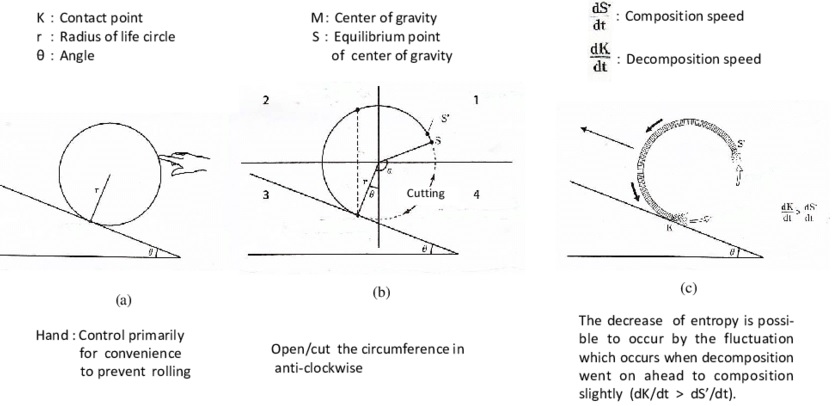
今、坂の上に、生命そのものを表している「生命の環」があると仮定します、転がり落ちないように、見えざる指が一時的に支えていると考えてください。そして、生命とは絶えず動的で、外部環境に向かって開いているものです。その開口部を通して、物質やエネルギー、情報が出入りしています。つまり、生命は開放系ですから、半径ｒの生命の環の円周の一部を開放することにします。

坂と環が接する接点ｋから開放するために円周を反時計回りに少しずつ削っていきます。すると、図のように円周の３分の１程度削ったところで、ある絶妙な均衡点が出現します。残された円弧の重心ｍは、接点ｋのちょうど真上に来ます。このとき、ぴたりと環が止まるのです。仮に見えざる指を円弧から離したとしても、環はバランスを保ったまま静止し、転がり落ちることはありません。ただ、それはすごく危ういバランスで止まっています。

この均衡点ｓから、さらに反時計回りに削っていきます。ここで指を離すと、残った環の重心ｍは少しだけ左側へずれ、環はぐらりと左へ傾こうとします。左に傾くということは、坂を少しだけ上り返したということです。この削り込む作業こそが、エントロピー増大の法則から先回りして分解する作業です。

このとき、円弧は生命の開いた環で、絶えず合成と分解が同時進行している動的平衡状態にあるとします。分解は断端ｋで起こり、合成は断端ｓ’で起こるとします。左にぐらりと傾いた円弧の断端ｋは、回転に伴って坂との接点から右側に飛び出します。飛び出した断端を接点に引き戻す程度の速度で、断端の分解（消失）が起こるとします。つまり、見かけ上、断端は飛び出すことなく常に接点から伸びないように見えるのです。

一方、断端ｓ’は、円弧の左回転にしたがって、左方向に引っ張られるように移動していきます。この移動速度を相殺する程度の速度で、断端ｓ’において新たな合成が起きるとします。つまり、断端ｋで分解が起こり、断端ｓ’で合成が起きている。この合成と分解のスピードがまったく同じなら、この円弧のバランスは釣り合ったまま、坂に静止し続けるはずです。ところが、円弧の分解の速度（ｄｋ／ｄｔ）が円弧の合成の速度（ｄｓ’／ｄｔ）よりもほんの少しだけ速い（大きい）とすれば、つまり、分解がわずかに合成を「先回り」するように働くとすれば、円弧のモーメントは絶えず反時計回りに働くことになります。円弧は常に、左回りに回転しようとするわけです。それはすなわち、坂を上り返そうとする力が働くということ。つまり、エントロピー増大の法則に抵抗し、生命が坂を上るというモデルを作ることができるわけです。円弧は絶えず一端で分解され、他端で合成されているので、円弧自体はゆっくりと坂を上りながら回転し、消費されつつ、新生されることになります。

ただ、合成よりも分解の量の方が少しだけ多いということは、坂を上り返しながらも、環自体が少しずつ短くなっていくということです。つまり、生命の環の寿命には限界があるということ。ですから、自分自身の生命の環がなくなってしまう前に、私たちは次の世代に生命の環のバトンタッチすることで生命を連鎖させていくのです。

坂を上り返す、この動的な円弧を、「ベルクソンの弧」と名づけ、動的平衡の数理的な概念モデルとして提案しています。

 

福岡さんが動的平衡の仕組みをモデル化した「ベルクソンの弧」。合成と分解を繰り返すことで、エントロピー増大の法則の坂を上る。

 

 

 

 

 

 

」